Công Thức Tính Diện Tích Hình Chữ Nhật: Hướng Dẫn Chi Tiết & Bài Tập

Diện tích hình chữ nhật là một trong những kiến thức nền tảng quan trọng trong toán học, đặc biệt trong lĩnh vực hình học. Việc nắm vững công thức tính diện tích hình chữ nhật không chỉ giúp học sinh giải quyết các bài toán trong chương trình học mà còn có nhiều ứng dụng thiết thực trong cuộc sống hàng ngày. Từ việc tính toán diện tích sàn nhà, diện tích tường cần sơn, cho đến quy hoạch đất đai hay thiết kế nội thất, công thức này đều đóng vai trò then chốt.

Hình chữ nhật với bốn góc vuông và hai cặp cạnh đối diện bằng nhau là một trong những hình học cơ bản nhất mà chúng ta được làm quen từ những năm đầu tiểu học. Mặc dù có vẻ đơn giản, nhưng việc hiểu sâu về cách tính diện tích hình chữ nhật và ứng dụng linh hoạt trong các tình huống khác nhau lại là một kỹ năng quan trọng cần được rèn luyện.

Trong bài viết này, chúng tôi sẽ giúp bạn hiểu rõ về công thức tính diện tích hình chữ nhật, cách áp dụng công thức vào các dạng bài tập khác nhau, cùng với những mẹo hữu ích giúp tính toán nhanh chóng và chính xác. Bạn sẽ được hướng dẫn từ những khái niệm cơ bản nhất đến các ứng dụng thực tế, kèm theo nhiều ví dụ minh họa và bài tập thực hành để củng cố kiến thức.

Dù bạn là học sinh đang cần ôn tập cho kỳ thi, phụ huynh muốn hỗ trợ con em trong việc học, hay đơn giản là người muốn ôn lại kiến thức toán học cơ bản, bài viết này sẽ là nguồn tài liệu hữu ích và đáng tin cậy cho bạn.

1. Khái niệm cơ bản về hình chữ nhật

Hình chữ nhật là một hình học phẳng cơ bản thuộc nhóm tứ giác, được định nghĩa bởi những đặc điểm đặc trưng và dễ nhận biết. Trước khi đi vào công thức tính diện tích hình chữ nhật, chúng ta cần hiểu rõ về khái niệm và các đặc tính quan trọng của hình chữ nhật.

Định nghĩa hình chữ nhật

Hình chữ nhật là một tứ giác có bốn góc đều là góc vuông (90 độ). Đây là đặc điểm quan trọng nhất để nhận biết một hình chữ nhật. Ngoài ra, hình chữ nhật còn có hai cặp cạnh đối diện song song và bằng nhau về độ dài.

Trong hình chữ nhật ABCD, nếu A, B, C, D là bốn đỉnh của hình thì:

• Các góc A, B, C, D đều là góc vuông (90 độ)
• Cạnh AB song song và bằng cạnh DC
• Cạnh AD song song và bằng cạnh BC

Đặc điểm của hình chữ nhật

Hình chữ nhật có nhiều đặc điểm quan trọng giúp phân biệt nó với các hình học khác:

1. Bốn góc vuông: Tất cả các góc trong hình chữ nhật đều là 90 độ, tổng số đo các góc là 360 độ.
2. Hai cặp cạnh đối diện: Hình chữ nhật có hai cặp cạnh đối diện song song và bằng nhau. Cặp cạnh dài hơn được gọi là chiều dài, cặp cạnh ngắn hơn được gọi là chiều rộng.
3. Đường chéo: Hai đường chéo của hình chữ nhật bằng nhau và cắt nhau tại trung điểm, chia đôi lẫn nhau.
4. Tính đối xứng: Hình chữ nhật có hai trục đối xứng đi qua trung điểm của các cặp cạnh đối diện.
5. Trường hợp đặc biệt: Khi tất cả các cạnh của hình chữ nhật bằng nhau, nó trở thành hình vuông – một trường hợp đặc biệt của hình chữ nhật.

Các thuật ngữ quan trọng

Khi làm việc với hình chữ nhật và công thức tính diện tích hình chữ nhật, chúng ta cần nắm vững các thuật ngữ sau:

• Chiều dài (a): Là độ dài của cạnh dài nhất trong hình chữ nhật.
• Chiều rộng (b): Là độ dài của cạnh ngắn nhất trong hình chữ nhật.
• Đường chéo (d): Là đoạn thẳng nối hai đỉnh không kề nhau của hình chữ nhật.
• Chu vi (P): Là tổng độ dài của tất cả các cạnh, tính bằng công thức P = 2(a + b).
• Diện tích (S): Là độ lớn của mặt phẳng được giới hạn bởi hình chữ nhật, tính bằng công thức S = a × b.

Phân biệt hình chữ nhật với các hình học khác

Hình chữ nhật có thể dễ dàng bị nhầm lẫn với một số hình học khác, đặc biệt là hình vuông và hình thoi:

• Hình vuông: Là trường hợp đặc biệt của hình chữ nhật khi tất cả các cạnh bằng nhau.
• Hình thoi: Có bốn cạnh bằng nhau nhưng các góc không nhất thiết phải là góc vuông.
• Hình bình hành: Có hai cặp cạnh đối diện song song và bằng nhau, nhưng các góc không nhất thiết phải là góc vuông.

Việc hiểu rõ các khái niệm cơ bản về hình chữ nhật là nền tảng quan trọng để áp dụng chính xác công thức tính diện tích hình chữ nhật trong các bài toán và ứng dụng thực tế. Trong phần tiếp theo, chúng ta sẽ đi sâu vào công thức tính diện tích và cách áp dụng nó một cách hiệu quả.

2. Công thức tính diện tích hình chữ nhật

Diện tích là một khái niệm quan trọng trong hình học, đặc biệt khi nói đến các hình phẳng như hình chữ nhật. Công thức tính diện tích hình chữ nhật là một trong những công thức cơ bản nhất mà học sinh được làm quen từ cấp tiểu học, nhưng lại có ứng dụng rộng rãi trong nhiều lĩnh vực của cuộc sống.

Công thức cơ bản

Công thức tính diện tích hình chữ nhật được biểu diễn bằng phép nhân giữa chiều dài và chiều rộng của hình:

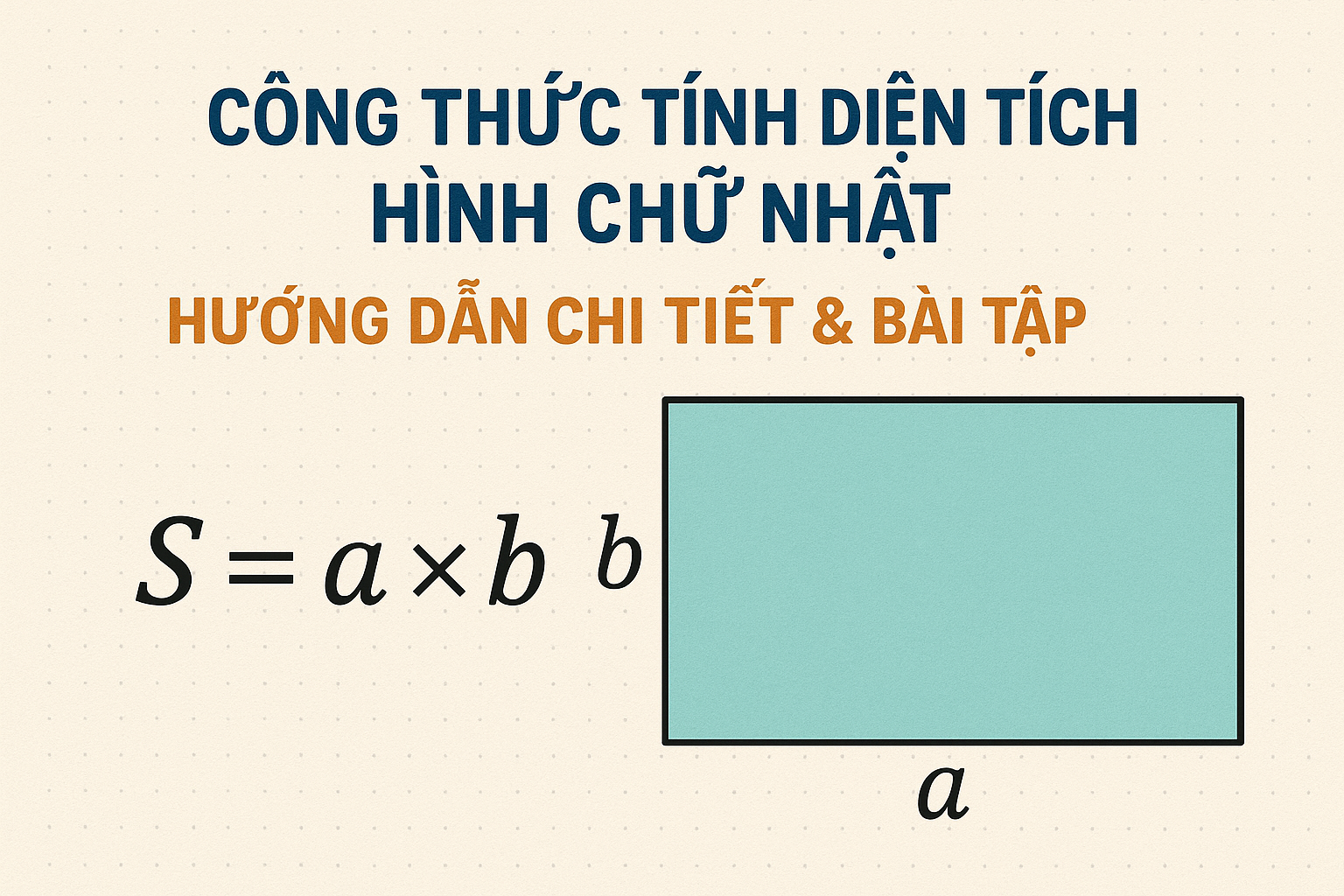
S = a × b

Trong đó:

• S là diện tích của hình chữ nhật
• a là chiều dài của hình chữ nhật
• b là chiều rộng của hình chữ nhật

Công thức này áp dụng cho mọi hình chữ nhật, không phụ thuộc vào kích thước hay tỷ lệ giữa chiều dài và chiều rộng. Đây là một công thức đơn giản nhưng vô cùng quan trọng trong toán học.

Ý nghĩa của công thức

Công thức tính diện tích hình chữ nhật S = a × b có ý nghĩa hình học rất rõ ràng. Diện tích của hình chữ nhật chính là số đơn vị diện tích (như cm², m²) mà hình đó chiếm trên mặt phẳng.

Nếu chia hình chữ nhật thành lưới ô vuông đơn vị, với mỗi ô có kích thước 1×1 đơn vị, thì diện tích của hình chữ nhật chính là tổng số ô vuông đơn vị nằm trong hình. Số lượng ô này bằng số ô theo chiều dài nhân với số ô theo chiều rộng, tương ứng với a × b.

Đây chính là lý do tại sao công thức tính diện tích hình chữ nhật lại là tích của chiều dài và chiều rộng. Công thức này phản ánh cấu trúc hình học cơ bản của hình chữ nhật và cách chúng ta đo lường không gian hai chiều.

Đơn vị đo diện tích

Khi áp dụng công thức tính diện tích hình chữ nhật, việc sử dụng đúng đơn vị đo là rất quan trọng. Đơn vị đo diện tích thường là đơn vị đo chiều dài bình phương:

• Mét vuông (m²): Đơn vị cơ bản trong hệ SI, thường dùng để đo diện tích phòng, nhà, đất…
• Centimét vuông (cm²): Thường dùng để đo diện tích các vật nhỏ, trang giấy…
• Kilomét vuông (km²): Dùng để đo diện tích lớn như thành phố, quốc gia…
• Hecta (ha): Bằng 10.000 m², thường dùng trong nông nghiệp, lâm nghiệp…
• Inch vuông (in²), foot vuông (ft²): Đơn vị đo trong hệ đo lường Anh-Mỹ

Khi tính toán, cần đảm bảo các kích thước (chiều dài và chiều rộng) được đo bằng cùng một đơn vị trước khi áp dụng công thức tính diện tích hình chữ nhật.

Chuyển đổi giữa các đơn vị đo diện tích

Trong nhiều tình huống, chúng ta cần chuyển đổi giữa các đơn vị đo diện tích khác nhau. Dưới đây là một số quy tắc chuyển đổi thông dụng:

• 1 m² = 10,000 cm²
• 1 km² = 1,000,000 m²
• 1 ha = 10,000 m²
• 1 ft² ≈ 0.093 m²
• 1 m² ≈ 10.764 ft²

Khi áp dụng công thức tính diện tích hình chữ nhật, nếu chiều dài và chiều rộng có đơn vị đo khác nhau, cần chuyển đổi chúng về cùng một đơn vị trước khi thực hiện phép nhân.

Ví dụ minh họa

Để hiểu rõ hơn về công thức tính diện tích hình chữ nhật, hãy xem xét một ví dụ đơn giản:

Ví dụ 1: Tính diện tích của một hình chữ nhật có chiều dài 5 cm và chiều rộng 3 cm.

Giải:

• Áp dụng công thức S = a × b
• Thay số: S = 5 cm × 3 cm = 15 cm²
• Vậy diện tích của hình chữ nhật là 15 cm²

Ví dụ 2: Tính diện tích của một mảnh đất hình chữ nhật có chiều dài 25 m và chiều rộng 12 m.

Giải:

• Áp dụng công thức S = a × b
• Thay số: S = 25 m × 12 m = 300 m²
• Vậy diện tích của mảnh đất là 300 m²

Công thức tính diện tích hình chữ nhật tuy đơn giản nhưng là nền tảng cho nhiều công thức tính diện tích phức tạp hơn của các hình khác. Hiểu rõ và áp dụng thành thạo công thức này sẽ giúp bạn giải quyết nhiều bài toán trong học tập cũng như các vấn đề thực tế trong cuộc sống.

3. Cách áp dụng công thức tính diện tích hình chữ nhật

Sau khi đã hiểu rõ về công thức tính diện tích hình chữ nhật S = a × b, việc áp dụng công thức này vào thực tế cần được thực hiện theo các bước cụ thể để đảm bảo kết quả chính xác. Trong phần này, chúng ta sẽ tìm hiểu chi tiết về cách áp dụng công thức, các trường hợp đặc biệt và những lưu ý quan trọng khi tính toán.

Các bước tính diện tích hình chữ nhật

Để áp dụng công thức tính diện tích hình chữ nhật một cách chính xác, bạn nên tuân theo các bước sau:

Bước 1: Xác định chiều dài và chiều rộng của hình chữ nhật

• Đo đạc hoặc xác định chiều dài (a) và chiều rộng (b) của hình chữ nhật
• Đảm bảo phân biệt đúng chiều dài (cạnh dài hơn) và chiều rộng (cạnh ngắn hơn)

Bước 2: Kiểm tra đơn vị đo

• Đảm bảo chiều dài và chiều rộng được đo bằng cùng một đơn vị
• Nếu khác đơn vị, cần chuyển đổi về cùng một đơn vị trước khi tính toán

Bước 3: Áp dụng công thức S = a × b

• Nhân chiều dài với chiều rộng để tính diện tích
• Ghi nhớ đơn vị của diện tích là đơn vị chiều dài bình phương (m², cm², km²…)

Bước 4: Kiểm tra kết quả

• Đánh giá tính hợp lý của kết quả (ví dụ: diện tích phải lớn hơn 0)
• Làm tròn kết quả theo yêu cầu của bài toán (nếu cần)

Ví dụ chi tiết với các bước giải

Ví dụ 1: Tính diện tích của một tấm bìa hình chữ nhật có chiều dài 45 cm và chiều rộng 30 cm.

Giải:

• Bước 1: Xác định chiều dài a = 45 cm và chiều rộng b = 30 cm
• Bước 2: Cả hai kích thước đều có cùng đơn vị là cm, nên không cần chuyển đổi
• Bước 3: Áp dụng công thức tính diện tích hình chữ nhật: S = a × b = 45 cm × 30 cm = 1.350 cm²
• Bước 4: Kết quả 1.350 cm² là hợp lý cho một tấm bìa kích thước như vậy

Ví dụ 2: Tính diện tích của một mảnh đất hình chữ nhật có chiều dài 25 m và chiều rộng 1.200 cm.

Giải:

• Bước 1: Xác định chiều dài a = 25 m và chiều rộng b = 1.200 cm
• Bước 2: Hai kích thước có đơn vị khác nhau, cần chuyển đổi về cùng đơn vị
  • Chuyển 1.200 cm = 12 m (vì 1 m = 100 cm)
• Bước 3: Áp dụng công thức tính diện tích hình chữ nhật: S = a × b = 25 m × 12 m = 300 m²
• Bước 4: Kết quả 300 m² là hợp lý cho một mảnh đất có kích thước như vậy

Trường hợp đặc biệt: Tính diện tích hình vuông

Hình vuông là trường hợp đặc biệt của hình chữ nhật khi chiều dài bằng chiều rộng. Trong trường hợp này, công thức tính diện tích hình chữ nhật trở thành:

S = a × a = a²

Trong đó a là độ dài cạnh của hình vuông.

Ví dụ: Tính diện tích của một hình vuông có cạnh dài 7 cm.

Giải:

• Áp dụng công thức diện tích hình vuông: S = a² = 7² = 49 cm²
• Vậy diện tích của hình vuông là 49 cm²

Cách kiểm tra kết quả tính toán

Sau khi áp dụng công thức tính diện tích hình chữ nhật, việc kiểm tra kết quả là rất quan trọng để tránh sai sót. Dưới đây là một số phương pháp kiểm tra:

1. Ước lượng sơ bộ: Làm tròn các kích thước để ước tính nhanh diện tích, sau đó so sánh với kết quả tính toán chính xác.
2. Kiểm tra đơn vị: Đảm bảo đơn vị của diện tích là đơn vị chiều dài bình phương (m², cm², km²…).
3. Kiểm tra tính hợp lý: Diện tích phải là số dương và phải nhỏ hơn diện tích của một hình chữ nhật lớn hơn đã biết.
4. Tính theo cách khác: Nếu có thể, hãy chia hình chữ nhật thành các phần nhỏ hơn, tính diện tích từng phần rồi cộng lại để kiểm tra.

Lưu ý khi áp dụng công thức

Khi áp dụng công thức tính diện tích hình chữ nhật, cần chú ý một số điểm sau:

1. Đơn vị đo: Luôn đảm bảo chiều dài và chiều rộng được đo bằng cùng một đơn vị trước khi nhân.
2. Phân biệt chiều dài và chiều rộng: Mặc dù kết quả không thay đổi khi hoán đổi chiều dài và chiều rộng trong công thức, nhưng việc phân biệt rõ ràng giúp tránh nhầm lẫn trong các bài toán phức tạp hơn.
3. Độ chính xác: Tùy thuộc vào yêu cầu của bài toán, kết quả có thể cần được làm tròn đến số thập phân cụ thể.
4. Hình chữ nhật không đều: Trong thực tế, không phải lúc nào hình chữ nhật cũng hoàn hảo. Khi đo đạc, có thể cần lấy giá trị trung bình của các cạnh đối diện.
5. Chuyển đổi đơn vị: Khi kết quả cần được biểu diễn bằng đơn vị khác với đơn vị tính toán, cần thực hiện chuyển đổi chính xác.

Việc nắm vững cách áp dụng công thức tính diện tích hình chữ nhật không chỉ giúp bạn giải quyết các bài toán trong trường học mà còn rất hữu ích trong nhiều tình huống thực tế. Từ việc tính diện tích sàn nhà để mua vật liệu lát nền, đến việc tính diện tích tường để mua sơn, công thức này luôn đóng vai trò quan trọng trong cuộc sống hàng ngày.

4. Các dạng bài tập về diện tích hình chữ nhật

Trong chương trình học toán từ cấp tiểu học đến trung học, học sinh sẽ gặp nhiều dạng bài tập khác nhau liên quan đến công thức tính diện tích hình chữ nhật. Việc nắm vững các dạng bài tập này không chỉ giúp học sinh đạt điểm cao trong các kỳ thi mà còn phát triển kỹ năng giải quyết vấn đề và tư duy logic. Dưới đây là các dạng bài tập phổ biến và cách giải quyết chúng.

Dạng 1: Tính diện tích khi biết chiều dài và chiều rộng

Đây là dạng bài tập cơ bản nhất, trực tiếp áp dụng công thức tính diện tích hình chữ nhật S = a × b.

Ví dụ 1: Tính diện tích hình chữ nhật có chiều dài 12 cm và chiều rộng 8 cm.

Hướng dẫn giải:

• Áp dụng công thức S = a × b
• Thay số: S = 12 cm × 8 cm = 96 cm²
• Vậy diện tích hình chữ nhật là 96 cm²

Ví dụ 2: Tính diện tích hình chữ nhật có chiều dài 2,5 m và chiều rộng 1,8 m.

Hướng dẫn giải:

• Áp dụng công thức S = a × b
• Thay số: S = 2,5 m × 1,8 m = 4,5 m²
• Vậy diện tích hình chữ nhật là 4,5 m²

Dạng 2: Tính chiều dài/chiều rộng khi biết diện tích và một cạnh

Trong dạng bài tập này, chúng ta cần biến đổi công thức tính diện tích hình chữ nhật để tìm chiều dài hoặc chiều rộng.

Nếu biết diện tích S và chiều rộng b, ta có thể tính chiều dài a: a = S ÷ b

Nếu biết diện tích S và chiều dài a, ta có thể tính chiều rộng b: b = S ÷ a

Ví dụ 3: Một hình chữ nhật có diện tích 120 cm² và chiều rộng 8 cm. Tính chiều dài của hình chữ nhật.

Hướng dẫn giải:

• Áp dụng công thức a = S ÷ b
• Thay số: a = 120 cm² ÷ 8 cm = 15 cm
• Vậy chiều dài của hình chữ nhật là 15 cm

Ví dụ 4: Một mảnh vườn hình chữ nhật có diện tích 350 m² và chiều dài 25 m. Tính chiều rộng của mảnh vườn.

Hướng dẫn giải:

• Áp dụng công thức b = S ÷ a
• Thay số: b = 350 m² ÷ 25 m = 14 m
• Vậy chiều rộng của mảnh vườn là 14 m

Dạng 3: Bài toán liên quan đến chu vi và diện tích

Dạng bài tập này kết hợp giữa công thức tính diện tích hình chữ nhật và công thức tính chu vi P = 2(a + b).

Ví dụ 5: Một hình chữ nhật có chu vi 50 cm và chiều rộng 10 cm. Tính diện tích của hình chữ nhật.

Hướng dẫn giải:

• Từ công thức chu vi: P = 2(a + b)
• Thay số: 50 = 2(a + 10)
• Giải phương trình: 50 = 2a + 20 → 2a = 30 → a = 15 cm
• Áp dụng công thức diện tích: S = a × b = 15 cm × 10 cm = 150 cm²
• Vậy diện tích hình chữ nhật là 150 cm²

Ví dụ 6: Một hình chữ nhật có chu vi 60 cm và diện tích 200 cm². Tính chiều dài và chiều rộng của hình chữ nhật.

Hướng dẫn giải:

• Từ công thức chu vi: P = 2(a + b) → a + b = P/2 = 60/2 = 30 cm
• Từ công thức diện tích: S = a × b → a × b = 200 cm²
• Ta có hệ phương trình:
  • a + b = 30
  • a × b = 200
• Từ phương trình thứ nhất: a = 30 – b
• Thay vào phương trình thứ hai: (30 – b) × b = 200
• Giải phương trình: 30b – b² = 200 → b² – 30b + 200 = 0
• Áp dụng công thức giải phương trình bậc hai: b = (30 ± √(900 – 800))/2 = (30 ± √100)/2 = (30 ± 10)/2
• b = 20 hoặc b = 10
• Nếu b = 20 thì a = 30 – 20 = 10
• Nếu b = 10 thì a = 30 – 10 = 20
• Vậy chiều dài và chiều rộng của hình chữ nhật là 20 cm và 10 cm

Dạng 4: Bài toán thực tế liên quan đến diện tích hình chữ nhật

Dạng bài tập này yêu cầu áp dụng công thức tính diện tích hình chữ nhật vào các tình huống thực tế.

Ví dụ 7: Một phòng học hình chữ nhật có chiều dài 8 m và chiều rộng 6 m. Người ta muốn lát nền phòng bằng các tấm gạch hình vuông cạnh 40 cm. Hỏi cần bao nhiêu tấm gạch?

Hướng dẫn giải:

• Tính diện tích phòng học: S = 8 m × 6 m = 48 m²
• Chuyển đổi đơn vị: 48 m² = 480.000 cm²
• Tính diện tích một tấm gạch: S₁ = 40 cm × 40 cm = 1.600 cm²
• Số tấm gạch cần thiết: 480.000 ÷ 1.600 = 300 tấm
• Vậy cần 300 tấm gạch để lát nền phòng học

Ví dụ 8: Một mảnh đất hình chữ nhật có chiều dài 25 m và chiều rộng 15 m. Người ta dùng 1/5 diện tích để xây nhà, phần còn lại làm vườn. Tính diện tích phần làm vườn.

Hướng dẫn giải:

• Tính diện tích mảnh đất: S = 25 m × 15 m = 375 m²
• Diện tích phần xây nhà: S₁ = 375 m² × 1/5 = 75 m²
• Diện tích phần làm vườn: S₂ = 375 m² – 75 m² = 300 m²
• Vậy diện tích phần làm vườn là 300 m²

Việc thực hành nhiều dạng bài tập khác nhau về công thức tính diện tích hình chữ nhật sẽ giúp học sinh phát triển kỹ năng giải quyết vấn đề và áp dụng kiến thức toán học vào các tình huống thực tế. Đồng thời, điều này cũng giúp củng cố hiểu biết về các khái niệm hình học cơ bản và phát triển tư duy logic.

5. Mẹo và kỹ thuật tính diện tích hình chữ nhật nhanh chóng

Mặc dù công thức tính diện tích hình chữ nhật S = a × b là khá đơn giản, nhưng trong nhiều tình huống, đặc biệt là khi giải quyết các bài toán phức tạp hoặc tính toán nhanh, việc áp dụng một số mẹo và kỹ thuật có thể giúp bạn tiết kiệm thời gian và tránh sai sót. Dưới đây là những mẹo hữu ích khi áp dụng công thức tính diện tích hình chữ nhật.

Kỹ thuật ước lượng diện tích

Trong nhiều tình huống thực tế, việc ước lượng diện tích trước khi tính toán chính xác là rất hữu ích. Điều này giúp bạn kiểm tra nhanh tính hợp lý của kết quả sau khi tính toán.

Mẹo 1: Làm tròn số

• Làm tròn chiều dài và chiều rộng đến số dễ tính toán
• Nhân các số đã làm tròn để có ước lượng nhanh
• So sánh với kết quả tính toán chính xác để kiểm tra

Ví dụ: Ước lượng diện tích hình chữ nhật có chiều dài 9,7 m và chiều rộng 4,3 m.

• Làm tròn: 9,7 m ≈ 10 m và 4,3 m ≈ 4 m
• Ước lượng: S ≈ 10 m × 4 m = 40 m²
• Kết quả chính xác: S = 9,7 m × 4,3 m = 41,71 m²
• Ước lượng khá gần với kết quả chính xác, chứng tỏ phép tính có khả năng đúng

Mẹo tính toán nhanh với các số tròn

Khi áp dụng công thức tính diện tích hình chữ nhật với các số đặc biệt, bạn có thể sử dụng một số mẹo tính nhanh sau:

Mẹo 2: Nhân với 10, 100, 1000…

• Khi nhân với 10: thêm một số 0 vào cuối
• Khi nhân với 100: thêm hai số 0 vào cuối
• Khi nhân với 1000: thêm ba số 0 vào cuối

Ví dụ: Tính diện tích hình chữ nhật có chiều dài 25 m và chiều rộng 10 m.

• S = 25 m × 10 m = 25 × 10 m² = 250 m² (thêm một số 0 vào 25)

Mẹo 3: Nhân với 5

• Nhân với 5 bằng cách nhân với 10 rồi chia 2

Ví dụ: Tính diện tích hình chữ nhật có chiều dài 16 m và chiều rộng 5 m.

• S = 16 m × 5 m = 16 × 5 m² = (16 × 10) ÷ 2 = 160 ÷ 2 = 80 m²

Mẹo 4: Nhân với 25

• Nhân với 25 bằng cách nhân với 100 rồi chia 4

Ví dụ: Tính diện tích hình chữ nhật có chiều dài 12 m và chiều rộng 25 cm.

• Chuyển đổi: 25 cm = 0,25 m
• S = 12 m × 0,25 m = 12 × 0,25 m² = (12 × 100) ÷ 4 = 1200 ÷ 4 = 300 m²

Cách sử dụng công cụ hỗ trợ

Trong thời đại công nghệ, có nhiều công cụ có thể hỗ trợ việc áp dụng công thức tính diện tích hình chữ nhật một cách nhanh chóng và chính xác.

Mẹo 5: Sử dụng máy tính

• Máy tính bỏ túi hoặc ứng dụng máy tính trên điện thoại là công cụ đơn giản nhất
• Đảm bảo nhập đúng số và đơn vị
• Kiểm tra kết quả bằng cách ước lượng

Mẹo 6: Sử dụng ứng dụng chuyên dụng

• Có nhiều ứng dụng di động và trang web chuyên về tính toán hình học
• Các ứng dụng này thường có giao diện trực quan, chỉ cần nhập kích thước và nhận kết quả
• Một số ứng dụng còn hỗ trợ chuyển đổi đơn vị tự động

Mẹo 7: Sử dụng bảng tính

• Excel hoặc Google Sheets rất hữu ích khi cần tính diện tích nhiều hình chữ nhật
• Tạo công thức một lần và áp dụng cho nhiều trường hợp
• Dễ dàng thay đổi kích thước và xem kết quả cập nhật tức thì

Phương pháp kiểm tra chéo kết quả

Sau khi áp dụng công thức tính diện tích hình chữ nhật, việc kiểm tra kết quả là rất quan trọng để đảm bảo tính chính xác.

Mẹo 8: Kiểm tra bằng phép chia

• Nếu S = a × b, thì a = S ÷ b và b = S ÷ a
• Sau khi tính S, hãy kiểm tra lại bằng cách tính a = S ÷ b và so sánh với giá trị a ban đầu

Mẹo 9: Kiểm tra đơn vị

• Đảm bảo đơn vị của diện tích là đơn vị chiều dài bình phương
• Ví dụ: nếu chiều dài và chiều rộng đo bằng mét, diện tích phải là mét vuông

Mẹo 10: Vẽ hình minh họa

• Vẽ hình chữ nhật theo tỷ lệ với kích thước đã cho
• Chia hình thành các ô vuông đơn vị để kiểm tra diện tích

Cách tránh các lỗi thường gặp khi tính diện tích

Khi áp dụng công thức tính diện tích hình chữ nhật, có một số lỗi thường gặp mà bạn nên tránh:

Lỗi 1: Nhầm lẫn đơn vị đo

• Đảm bảo chiều dài và chiều rộng có cùng đơn vị đo trước khi nhân
• Ghi nhớ đơn vị của diện tích là đơn vị chiều dài bình phương

Lỗi 2: Nhầm lẫn giữa chu vi và diện tích

• Chu vi là tổng độ dài các cạnh: P = 2(a + b)
• Diện tích là phần mặt phẳng bên trong hình: S = a × b

Lỗi 3: Sai sót khi chuyển đổi đơn vị

• Khi chuyển từ cm sang m, chia cho 100 (không phải 10)
• Khi chuyển từ m² sang cm², nhân với 10.000 (không phải 100)

Lỗi 4: Không kiểm tra tính hợp lý của kết quả

• Diện tích phải là số dương
• Diện tích phải nhỏ hơn diện tích của một hình lớn hơn đã biết

Việc áp dụng các mẹo và kỹ thuật này khi sử dụng công thức tính diện tích hình chữ nhật sẽ giúp bạn tính toán nhanh chóng, chính xác và tránh được những sai sót thường gặp. Đặc biệt trong các kỳ thi hoặc khi giải quyết các vấn đề thực tế, những kỹ năng này sẽ rất hữu ích.

6. Ứng dụng thực tế của công thức tính diện tích hình chữ nhật

Công thức tính diện tích hình chữ nhật không chỉ là một công thức toán học đơn thuần mà còn có rất nhiều ứng dụng thực tế trong cuộc sống hàng ngày và trong nhiều ngành nghề khác nhau. Hiểu và áp dụng đúng công thức này sẽ giúp chúng ta giải quyết nhiều vấn đề thực tiễn một cách hiệu quả. Dưới đây là những ứng dụng phổ biến của công thức tính diện tích hình chữ nhật trong các lĩnh vực khác nhau.

Ứng dụng trong kiến trúc và xây dựng

Trong lĩnh vực kiến trúc và xây dựng, công thức tính diện tích hình chữ nhật được sử dụng rộng rãi và là công cụ không thể thiếu:

Tính toán vật liệu xây dựng:

• Tính diện tích sàn để xác định số lượng gạch lát nền cần thiết
• Tính diện tích tường để ước tính lượng sơn, giấy dán tường hoặc gạch ốp
• Tính diện tích mái nhà để xác định số lượng ngói hoặc tấm lợp cần thiết

Ví dụ thực tế: Một căn phòng có chiều dài 5,5 m và chiều rộng 4 m cần được lát gạch. Mỗi tấm gạch có kích thước 50 cm × 50 cm.

• Diện tích phòng: S = 5,5 m × 4 m = 22 m²
• Diện tích một tấm gạch: S₁ = 0,5 m × 0,5 m = 0,25 m²
• Số lượng gạch cần thiết: 22 m² ÷ 0,25 m² = 88 tấm
• Thêm 10% dự phòng: 88 + 8,8 ≈ 97 tấm

Thiết kế và quy hoạch:

• Tính diện tích các phòng trong nhà để đảm bảo đủ không gian sử dụng
• Tính diện tích khu đất để quy hoạch các công trình
• Tính diện tích mặt bằng để bố trí nội thất và thiết bị

Ứng dụng trong thiết kế nội thất

Trong thiết kế nội thất, công thức tính diện tích hình chữ nhật giúp tối ưu hóa không gian và lựa chọn đồ nội thất phù hợp:

Bố trí nội thất:

• Tính diện tích cần thiết cho các đồ nội thất như giường, tủ, bàn
• Xác định khoảng trống cần thiết để di chuyển trong phòng
• Tính toán diện tích tường trống để bố trí tranh ảnh, kệ sách

Ví dụ thực tế: Một phòng khách có diện tích 24 m². Bạn cần đặt một bộ sofa hình chữ nhật có kích thước 2,8 m × 1,6 m và một bàn trà 1,2 m × 0,6 m.

• Diện tích sofa: 2,8 m × 1,6 m = 4,48 m²
• Diện tích bàn trà: 1,2 m × 0,6 m = 0,72 m²
• Tổng diện tích đồ nội thất: 4,48 m² + 0,72 m² = 5,2 m²
• Diện tích còn lại để di chuyển: 24 m² – 5,2 m² = 18,8 m²

Lựa chọn vật liệu:

• Tính diện tích thảm trải sàn
• Tính diện tích rèm cửa cần thiết
• Tính diện tích bề mặt đồ nội thất cần sơn hoặc phủ vật liệu

Ứng dụng trong nông nghiệp và quy hoạch đất

Trong nông nghiệp và quy hoạch đất, công thức tính diện tích hình chữ nhật giúp tối ưu hóa việc sử dụng đất và tính toán năng suất:

Quy hoạch đất nông nghiệp:

• Tính diện tích các thửa ruộng, vườn để quy hoạch trồng trọt
• Tính diện tích cần tưới tiêu
• Ước tính sản lượng dựa trên diện tích canh tác

Ví dụ thực tế: Một thửa ruộng hình chữ nhật có chiều dài 100 m và chiều rộng 50 m được dùng để trồng lúa. Năng suất trung bình là 5 tấn/ha.

• Diện tích ruộng: S = 100 m × 50 m = 5.000 m² = 0,5 ha
• Sản lượng ước tính: 0,5 ha × 5 tấn/ha = 2,5 tấn lúa

Quy hoạch đô thị:

• Tính diện tích các lô đất để phân lô bán nền
• Tính diện tích công viên, khu vui chơi trong đô thị
• Tính diện tích đường giao thông, bãi đỗ xe

Ứng dụng trong đời sống hàng ngày

Trong cuộc sống hàng ngày, chúng ta thường xuyên áp dụng công thức tính diện tích hình chữ nhật mà đôi khi không nhận ra:

Mua sắm và trang trí:

• Tính diện tích khăn trải bàn cần mua
• Tính diện tích giấy gói quà
• Tính diện tích vải may rèm cửa

Ví dụ thực tế: Bạn cần mua vải để may rèm cho một cửa sổ cao 2,2 m và rộng 1,5 m. Rèm cần dài hơn cửa sổ 20 cm và rộng hơn 30 cm mỗi bên.

• Chiều cao rèm: 2,2 m + 0,2 m = 2,4 m
• Chiều rộng rèm: 1,5 m + 0,3 m × 2 = 2,1 m
• Diện tích vải cần mua: 2,4 m × 2,1 m = 5,04 m²

Sửa chữa và cải tạo nhà:

• Tính diện tích sàn cần thay mới
• Tính diện tích tường cần sơn
• Tính diện tích trần nhà cần làm mới

Làm vườn:

• Tính diện tích bãi cỏ cần trồng
• Tính diện tích luống hoa, luống rau
• Tính lượng phân bón cần thiết dựa trên diện tích

Ví dụ thực tế về cách áp dụng công thức

Ví dụ 1: Tính chi phí sơn tường

Một căn phòng hình chữ nhật có chiều dài 6 m, chiều rộng 4 m và chiều cao 3 m. Phòng có 1 cửa ra vào kích thước 2 m × 0,9 m và 2 cửa sổ mỗi cái kích thước 1,5 m × 1,2 m. Tính diện tích tường cần sơn và chi phí sơn nếu 1 lít sơn phủ được 8 m² và giá sơn là 200.000 đồng/lít.

Giải:

• Diện tích 4 bức tường: 2 × (6 m × 3 m) + 2 × (4 m × 3 m) = 36 m² + 24 m² = 60 m²
• Diện tích cửa ra vào: 2 m × 0,9 m = 1,8 m²
• Diện tích 2 cửa sổ: 2 × (1,5 m × 1,2 m) = 3,6 m²
• Diện tích tường cần sơn: 60 m² – 1,8 m² – 3,6 m² = 54,6 m²
• Lượng sơn cần thiết: 54,6 m² ÷ 8 m²/lít = 6,825 lít ≈ 7 lít
• Chi phí sơn: 7 lít × 200.000 đồng/lít = 1.400.000 đồng

Ví dụ 2: Tính chi phí lát sàn

Một căn hộ có phòng khách hình chữ nhật kích thước 5 m × 4 m và phòng ngủ hình chữ nhật kích thước 4 m × 3,5 m. Chủ nhà muốn lát sàn gỗ với giá 350.000 đồng/m². Tính tổng chi phí lát sàn cho hai phòng.

Giải:

• Diện tích phòng khách: 5 m × 4 m = 20 m²
• Diện tích phòng ngủ: 4 m × 3,5 m = 14 m²
• Tổng diện tích cần lát sàn: 20 m² + 14 m² = 34 m²
• Tổng chi phí: 34 m² × 350.000 đồng/m² = 11.900.000 đồng

Những ví dụ thực tế này cho thấy công thức tính diện tích hình chữ nhật có vai trò quan trọng trong nhiều hoạt động hàng ngày, từ việc tính toán chi phí xây dựng, sửa chữa nhà cửa đến quy hoạch không gian sống và làm việc. Việc nắm vững công thức này và biết cách áp dụng linh hoạt sẽ giúp chúng ta tiết kiệm thời gian, công sức và chi phí trong nhiều tình huống thực tế.

7. Câu hỏi thường gặp về diện tích hình chữ nhật

Khi học về công thức tính diện tích hình chữ nhật, học sinh và nhiều người thường gặp phải một số thắc mắc. Dưới đây là những câu hỏi thường gặp và câu trả lời chi tiết để giúp bạn hiểu rõ hơn về chủ đề này.

Làm thế nào để phân biệt chiều dài và chiều rộng của hình chữ nhật?

Theo quy ước, chiều dài của hình chữ nhật là cạnh dài hơn, còn chiều rộng là cạnh ngắn hơn. Tuy nhiên, trong công thức tính diện tích hình chữ nhật S = a × b, việc xác định cạnh nào là chiều dài, cạnh nào là chiều rộng không ảnh hưởng đến kết quả tính diện tích, vì phép nhân có tính chất giao hoán (a × b = b × a).

Trong thực tế, việc phân biệt chiều dài và chiều rộng thường dựa vào:

• Hướng nhìn hoặc hướng sử dụng của vật thể
• Quy ước trong từng lĩnh vực cụ thể (ví dụ: trong kiến trúc, chiều dài thường là cạnh song song với mặt tiền)
• Tỷ lệ kích thước (cạnh dài hơn được gọi là chiều dài)

Điều quan trọng là phải nhất quán trong cách gọi tên các cạnh khi giải quyết một bài toán cụ thể.

Tại sao diện tích hình chữ nhật lại bằng tích của chiều dài và chiều rộng?

Công thức tính diện tích hình chữ nhật S = a × b có thể được hiểu một cách trực quan thông qua mô hình lưới ô vuông. Nếu chia hình chữ nhật thành các ô vuông đơn vị, với mỗi ô có kích thước 1×1 đơn vị, thì:

• Số ô theo chiều dài sẽ là a ô
• Số ô theo chiều rộng sẽ là b ô
• Tổng số ô trong hình chữ nhật sẽ là a × b ô

Mỗi ô vuông đơn vị có diện tích là 1 đơn vị diện tích, nên tổng diện tích của hình chữ nhật sẽ là a × b đơn vị diện tích.

Về mặt toán học, diện tích là đại lượng đo độ lớn của mặt phẳng hai chiều. Phép nhân giữa hai kích thước (chiều dài và chiều rộng) chính là cách để tính toán độ lớn này.

Làm thế nào để tính diện tích hình chữ nhật khi các cạnh có đơn vị đo khác nhau?

Khi áp dụng công thức tính diện tích hình chữ nhật với các cạnh có đơn vị đo khác nhau, bạn cần chuyển đổi chúng về cùng một đơn vị trước khi thực hiện phép nhân. Dưới đây là các bước thực hiện:

1. Chọn một đơn vị đo chung (thường là đơn vị nhỏ hơn để tránh số thập phân phức tạp)
2. Chuyển đổi tất cả các kích thước về đơn vị đã chọn
3. Áp dụng công thức S = a × b với các giá trị đã chuyển đổi
4. Ghi kết quả với đơn vị diện tích tương ứng (đơn vị chiều dài bình phương)

Ví dụ: Tính diện tích hình chữ nhật có chiều dài 2 m và chiều rộng 50 cm.

Giải:

• Chuyển đổi về cùng đơn vị: 2 m = 200 cm
• Áp dụng công thức: S = 200 cm × 50 cm = 10.000 cm²
• Có thể chuyển đổi kết quả: 10.000 cm² = 1 m²

Ngoài ra, bạn cũng có thể chuyển đổi cả hai kích thước về đơn vị mét:

• 50 cm = 0,5 m
• S = 2 m × 0,5 m = 1 m²

Có cách nào khác để tính diện tích hình chữ nhật ngoài công thức S = a × b không?

Mặc dù công thức tính diện tích hình chữ nhật S = a × b là cách phổ biến nhất, nhưng trong một số trường hợp đặc biệt, có thể sử dụng các phương pháp khác:

1. Từ nửa chu vi và tỷ lệ cạnh:
   • Nếu biết nửa chu vi p = (a + b) và tỷ lệ a:b
   • Ta có thể tính a và b, sau đó áp dụng công thức S = a × b
2. Từ đường chéo và góc giữa đường chéo:
   • Nếu biết độ dài đường chéo d và góc θ giữa đường chéo và một cạnh
   • S = (d² × sin θ × cos θ) / 2
3. Từ chu vi và diện tích tối đa:
   • Nếu biết chu vi P, hình chữ nhật có diện tích lớn nhất khi là hình vuông
   • Khi đó a = b = P/4 và S = (P/4)²
4. Phương pháp chia nhỏ:
   • Chia hình chữ nhật thành các hình chữ nhật nhỏ hơn
   • Tính diện tích từng phần và cộng lại
5. Phương pháp đếm ô vuông:
   • Vẽ hình chữ nhật trên giấy ô vuông
   • Đếm số ô vuông nằm trong hình

Tuy nhiên, công thức tính diện tích hình chữ nhật S = a × b vẫn là phương pháp đơn giản và hiệu quả nhất trong hầu hết các trường hợp.

Làm thế nào để áp dụng công thức tính diện tích hình chữ nhật vào các bài toán phức tạp?

Để áp dụng công thức tính diện tích hình chữ nhật vào các bài toán phức tạp, bạn có thể sử dụng các chiến lược sau:

1. Phân tích bài toán:
   • Xác định rõ thông tin đã cho và thông tin cần tìm
   • Vẽ hình minh họa để hình dung bài toán rõ ràng hơn
2. Chia nhỏ vấn đề:
   • Đối với hình phức tạp, chia thành các hình chữ nhật đơn giản
   • Tính diện tích từng phần và kết hợp kết quả (cộng hoặc trừ)
3. Sử dụng phương trình và hệ phương trình:
   • Khi bài toán liên quan đến nhiều biến số
   • Thiết lập các phương trình dựa trên các điều kiện đã cho
4. Áp dụng kiến thức bổ sung:
   • Kết hợp với các công thức khác như công thức tính chu vi, định lý Pythagoras
   • Sử dụng tính chất của hình chữ nhật (đường chéo bằng nhau, góc vuông)
5. Kiểm tra tính hợp lý:
   • Đánh giá kết quả dựa trên ước lượng và kinh nghiệm
   • Thử nghiệm với các giá trị đặc biệt để kiểm tra công thức

Ví dụ bài toán phức tạp: Một mảnh đất hình chữ nhật có chu vi 100 m. Người ta dựng hàng rào xung quanh với chi phí 200.000 đồng/m cho cạnh dài và 150.000 đồng/m cho cạnh ngắn. Tổng chi phí làm hàng rào là 4.200.000 đồng. Tính diện tích mảnh đất.

Giải:

• Gọi a là chiều dài, b là chiều rộng của mảnh đất
• Từ chu vi: 2a + 2b = 100 → a + b = 50 (1)
• Từ chi phí hàng rào: 2a × 200.000 + 2b × 150.000 = 4.200.000
• Rút gọn: 400.000a + 300.000b = 4.200.000
• Chia cho 100.000: 4a + 3b = 42 (2)
• Từ (1): a = 50 – b
• Thay vào (2): 4(50 – b) + 3b = 42
• Giải: 200 – 4b + 3b = 42 → 200 – b = 42 → b = 158
• Từ (1): a = 50 – 158 = -108

Kết quả a âm không hợp lý, nên ta đổi vai trò a và b:

• Từ (1): b = 50 – a
• Thay vào (2): 4a + 3(50 – a) = 42
• Giải: 4a + 150 – 3a = 42 → a + 150 = 42 → a = -108

Kết quả vẫn không hợp lý. Kiểm tra lại bài toán, ta thấy có sự nhầm lẫn trong cách hiểu đề bài. Giả sử a là chiều dài, b là chiều rộng:

• Chi phí làm hàng rào: 2a × 200.000 + 2b × 150.000 = 4.200.000
• Từ chu vi: a + b = 50
• Thay b = 50 – a vào phương trình chi phí:
• 2a × 200.000 + 2(50 – a) × 150.000 = 4.200.000
• 400.000a + 15.000.000 – 300.000a = 4.200.000
• 100.000a = 4.200.000 – 15.000.000 = -10.800.000
• a = -108

Kết quả vẫn không hợp lý. Có thể đề bài có sai sót hoặc cần hiểu theo cách khác.

Giả sử đề bài là: Chi phí làm hàng rào là 200.000 đồng/m cho cạnh dài và 150.000 đồng/m cho cạnh ngắn. Tổng chi phí là 4.200.000 đồng.

• Chi phí: 2a × 200.000 + 2b × 150.000 = 4.200.000
• Từ chu vi: 2a + 2b = 100
• Rút gọn: a + b = 50
• Từ phương trình chi phí: 400.000a + 300.000b = 4.200.000
• Chia cho 100.000: 4a + 3b = 42
• Lập hệ phương trình:
  • a + b = 50
  • 4a + 3b = 42
• Nhân phương trình (1) với 4: 4a + 4b = 200
• Trừ phương trình (2): 4b – 3b = 200 – 42 → b = 158
• Thay vào (1): a + 158 = 50 → a = 30

Vậy chiều dài a = 30 m, chiều rộng b = 20 m. Diện tích mảnh đất: S = a × b = 30 m × 20 m = 600 m²

Những câu hỏi thường gặp này và câu trả lời chi tiết sẽ giúp bạn hiểu sâu hơn về công thức tính diện tích hình chữ nhật và cách áp dụng nó trong các tình huống khác nhau. Việc nắm vững những kiến thức này sẽ giúp bạn tự tin hơn khi giải quyết các bài toán liên quan đến diện tích hình chữ nhật trong học tập cũng như trong cuộc sống thực tế.

8. Kết luận

Công thức tính diện tích hình chữ nhật là một trong những công thức cơ bản nhất trong toán học, nhưng lại có tầm quan trọng vô cùng lớn trong cuộc sống hàng ngày. Qua bài viết này, chúng ta đã cùng nhau khám phá chi tiết về công thức S = a × b, từ khái niệm cơ bản đến các ứng dụng thực tế đa dạng.

Chúng ta đã tìm hiểu về đặc điểm của hình chữ nhật với bốn góc vuông và hai cặp cạnh đối diện bằng nhau, hiểu rõ ý nghĩa của công thức diện tích và cách áp dụng nó một cách chính xác. Qua các ví dụ minh họa và bài tập thực hành, chúng ta đã thấy được cách giải quyết nhiều dạng bài toán khác nhau liên quan đến diện tích hình chữ nhật, từ những bài toán đơn giản đến phức tạp.

Những mẹo và kỹ thuật tính toán nhanh chóng đã được chia sẻ để giúp bạn tiết kiệm thời gian và tránh sai sót khi áp dụng công thức tính diện tích hình chữ nhật. Đặc biệt, chúng ta đã khám phá nhiều ứng dụng thực tế của công thức này trong kiến trúc, xây dựng, thiết kế nội thất, nông nghiệp và đời sống hàng ngày.

Phần câu hỏi thường gặp đã giải đáp những thắc mắc phổ biến, giúp bạn hiểu sâu hơn về các khía cạnh khác nhau của công thức tính diện tích hình chữ nhật và cách áp dụng linh hoạt trong nhiều tình huống.

Việc nắm vững công thức tính diện tích hình chữ nhật không chỉ giúp học sinh đạt điểm cao trong các kỳ thi mà còn là kỹ năng thiết yếu trong cuộc sống. Từ việc tính toán vật liệu xây dựng, thiết kế không gian sống, đến quy hoạch đất đai và nhiều hoạt động khác, công thức này luôn đóng vai trò quan trọng.

Hy vọng rằng bài viết này đã cung cấp cho bạn kiến thức đầy đủ và hữu ích về công thức tính diện tích hình chữ nhật. Hãy thực hành thường xuyên với các bài tập đã được giới thiệu để củng cố kiến thức và phát triển kỹ năng tính toán của mình.

Bạn đã sẵn sàng áp dụng công thức tính diện tích hình chữ nhật vào học tập và cuộc sống của mình chưa? Hãy bắt đầu với những bài toán đơn giản và dần dần tiến đến những ứng dụng phức tạp hơn. Chúc bạn thành công!